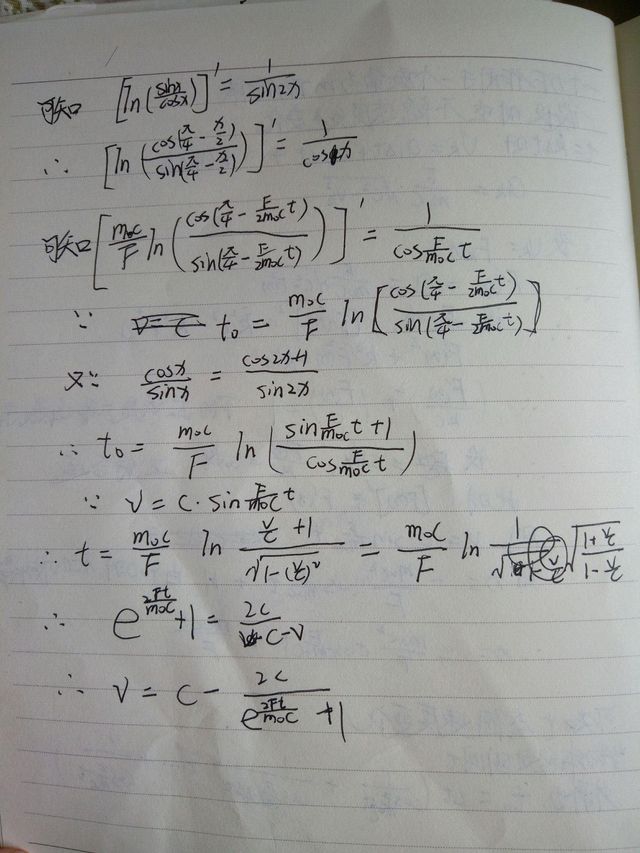我在高中时数学挺好的。

像是一般的试卷考试，标准时间是两个小时。我最快能在 40+ 分钟完成，同时分数也能到 135 分往上。曾记得有次我做完了一张试卷，同桌才做完了一半，把他惊得够呛。

但我一直想成为的是物理学家。把物理上的问题，用数学的方法去解出来，真的是一件很有成就感的事情。

我并没有学过什么物理数学竞赛的知识，积分也只是最简单的 △t，也更不会大学里面的找原函数的方法，都是凭借于自己的感觉，沉溺于自己推导各种高于高中的公式，也曾花费了比较多的高中时光。

那么话说到此，看看我都做了些什么吧~

下面简单列三个问题哈，图片都是来源于当时的草稿或笔记，所用的所有知识也都仅限于高中水平~

ps. 请原谅我那被老师评价为鸡爪子挠一样的字

小球下落速度

当一个球速度为 0 开始下落时，它受到的阻力 $f_n$ 与速度成正比,即 $f_n = kV$ ，那它下落时速度与时间的公式。

我计算得出是下面的公式：

在我计算得出后，我会先进行一轮验算：

假设空气阻力的系数为 0 时，根据上面的公式可以得出 $V_n = gt$

当时间无穷大时，最大速度为 $V_{max}=\frac{mg}{k}$

嘿! 上面的结论显然都是正确的，那这个结果就有很大概率也是正确的。在验算成功后，便是收获成就感的时刻。

半圆重心在哪里

一个半径为 $R$ 的半圆，它的重心在哪里。

最终算出的结果就是 $\frac{4R}{3\pi}$。

最开始我也是按照 x 轴或者 y 轴去一点点地算，因为质量分布不均而造成不好去计算，当然这种方法还是可以算得出来的。

后面想到了一个简单的办法，每一段圆弧都可以近似看成三角形，每一段圆弧的重心也就是三角形的重心。那么可以把半圆的重心等效为一个半径为 $\frac{2}{3}R$ 的圆弧的重心。

再求得圆弧的重心就相对简单了很多。

那天的画面我还留有印象。

在我计算成功后，我把好几张纸叠在一起，剪了一个厚一点的小圆片，把它切成半圆。然后我用笔在计算好的位置点了一个标志，然后用笔尖托起了这个半圆。

它稳稳的悬在了那里!

$E=mc^2$

接着就是经典的 $E=mc^2$。

这部分内容应该是在物理的一本选修上，那三个相对论的公式就列在那里，然后就列出了 $E=mc^2$。

总之这些公式就是对的。老师告诉我们，说牛顿的公式在高速情况下是不成立的，这些知识不是现在的公式能解决的，接着就匆匆一带而过了，

我看着那几个公式，开始大胆地想，牛顿的 $F=ma$ 以及公式 $W=Fx$ 在任一时刻都是成立的，只不过随着时间变化，$m$ 变了，$t$ 变了，$x$ 变了，所以这些公式才不成立。

接着凭着大胆的直觉，我觉得通过上面那三个变化公式加上牛顿的公式可以推导出 $E=mc^2$。

于是我就开始了大胆地算。

草稿太乱太多我就没有整理，在这里就只放出我最终汇总整理的计算过程吧，感兴趣的话可以点击图片查看细节。

这段计算过程是持续了好多天的，上课不听，下课不玩，光草稿好像都二十多张了。

当时应该是在高二结束的暑假，我们整体在富士康里上课。记得是一个很热的夏天，风扇在头顶呼啦呼啦地转。

算出来之后的成就感是无与伦比的，它也奠定了我对物理的所有信心。

在当时，我一心觉得，我考大学要选物理专业，我会成为一个物理学家。

关于这些

回看上面这些计算过程，可能当中也存在着错误，可能算得太麻烦。

有一些问题我费了很多劲自认为解出来了，也有很多问题会卡到一个点上无法继续，受限于我的知识水平。

当时我心中也存在着很多困惑。浪费这么多时间算这些高考不会考的问题划算吗？尤其是，你算了好麻烦，别人用你看不懂的方法几步算出来了，更何况这个问题你怎么知道用你现在的知识能解出来呢？

但这些，都是来源于我的想法，我觉得可以算出来，就试了下。

> 高中三年算出来一些挺有意思的问题，并且高中物理蛮好(尽管高考物理并不出色 T.T)

时空穿梭

不知不觉间，我已经工作两年了。

现在呢，如果我碰到了高中时期的我，我大概是不敢在他面前露面的，和他能说些什么呢？

未来你没有成为你想成为的物理学家，也没有从事物理相关的工作与研究。

你大学读的专业是电子信息，浑浑噩噩过了四年，高数甚至险些挂科。

本科一毕业你就去工作了，成为了互联网公司里最底层的螺丝钉，你干着前端写着业务加着班，做着和研究丝毫不搭边的工作。

我也只能说：

那么，用这张图来收尾吧~

---The End---

感谢阅读到这里。

忽然想再写一篇讲讲我是怎么走上前端这条路的，如果感兴趣的话，可以在下方留言哦~嘿嘿(^▽^)