二阶贝塞尔曲线的点击判定

2021-05-31coding bezier

引言

最近在做一个可视化项目时，有两点之间绘制链路的需求。考虑到可能有多条链路同时存在，因此选用了二阶贝塞尔曲线。但也有点击此曲线进行交互的功能，因此需要实现二阶贝塞尔曲线的点击判定。

贝塞尔曲线

贝塞尔曲线是一种曲线，用于计算机图形绘制，CSS动画等方面。贝塞尔曲线形状完全由控制点决定，有 $n$ 个控制点对应 $n-1$ 阶贝塞尔曲线。

一阶贝塞尔曲线

在给定两个控制点 $P_0$ 、 $P_1$ 的情况下，是两点之间直接连线构成的直线，由下列公式给出：

B(t)=P_0+(P_1-P_0 )t=(1-t) P_0+tP_1 , t∈[0,1]

二阶贝塞尔曲线

二阶贝塞尔曲线，有首末点分别为 $P_0$ 、 $P_2$ 的情况下，控制点为 $P_1$ ，由下列公式给出：

B(t)=(1-t)^2 P_0+2t(1-t) P_1+t^2 P_2 , t∈[0,1]

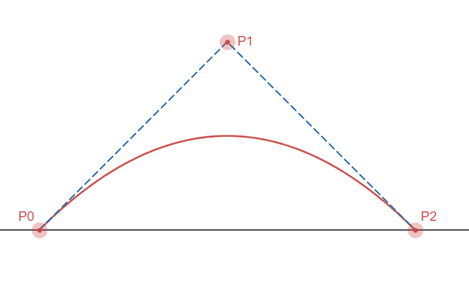
点到二阶贝塞尔曲线的准确距离计算

假设有一个二阶贝塞尔曲线，你在这个曲线上旁边点了一点，怎么获得点到这个曲线的最短距离呢？可以将你点击的位置视作圆心，半径向外不断扩大这个圆，直到这个圆与曲线只有一个交点时，此时这个圆与曲线相切，见上方图片位置。

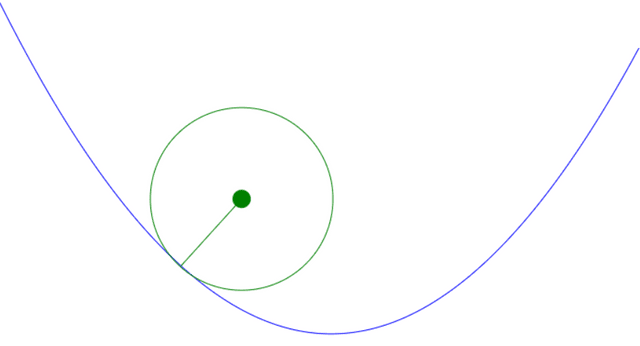
设二阶贝塞尔曲线三个控制点分别为 $P_0$ 、 $P_1$ 、 $P_2$ ，点击点位置为 $P_i$ ，与圆相切位置为 $P_t$ ，相切点对应 $t$ 值为 $t_0$ ，贝塞尔曲线x轴y轴方向关于t的导数分别为 $X'(t)$ 、 $Y'(t)$ 。因为相切，向量乘积为0，则应满足以下方程：

X'(t)*(x_i-x_t) + Y'(t)*(y_i - y_t) = 0 \qquad (1)

由二阶贝塞尔曲线满足：

B(t)=(P_0-2P_1+P_2)t^2 + 2*(P_1-P_0)t+P_0

B'(t)=2*(P_0-2P_1+P_2)t+ 2*(P_1-P_0)

易知以上方程可以化为 $At^3+Bt^2+Ct+D=0$ 的形式，是一个一元三次方程。
$P_0$ 点的x轴坐标为 $x_0$ ，y轴坐标为 $y_0$ ，其余点同理。为了方便计算，定义如下变量：

\left\{ \begin{align*} & (a_0, a_1)=P_1-P_0 \\ & (b_0, b_1)=P_0-2P_1+P_2 \\ \end{align*} \right.

则公式 (1) 通过相关软件可以简单化简为以下公式：

(b_0^2 + b_1^2)*t^3 + (3*a_0*b_0 + 3*a_1*b_1)*t^2 + [2*a_0^2 + 2*a_1^2 + b_0*(x_0 - x_i) + b_1*(y_0 - y_i)]*t + a_0*(x_0 - x_i) + a_1*(y_0 - y_i) = 0

接着根据一元三次方程求根公式，可以进一步计算得出对应的 $t$ 的值，进而计算出准确距离。

代码实现

搜索可以得到二阶贝塞尔曲线距离计算相关实现实例，其代码中已进行了一些性能优化。因此将其”翻译”到js语言，源代码如下：

// The MIT License
// Copyright © 2018 Inigo Quilez
// Distance to a quadratic bezier segment, which can be solved analyically with a cubic.
// List of some other 2D distances: https://www.shadertoy.com/playlist/MXdSRf
// and www.iquilezles.org/www/articles/distfunctions2d/distfunctions2d.htm
float dot2( in vec2 v ) { return dot(v,v); }
float cross2( in vec2 a, in vec2 b ) { return a.x*b.y - a.y*b.x; }
    
// unsigned distance to a quadratic bezier
float udBezier( in vec2 pos, in vec2 A, in vec2 B, in vec2 C )
{    
    vec2 a = B - A;
    vec2 b = A - 2.0*B + C;
    vec2 c = a * 2.0;
    vec2 d = A - pos;

    float kk = 1.0/dot(b,b);
    float kx = kk * dot(a,b);
    float ky = kk * (2.0*dot(a,a)+dot(d,b))/3.0;
    float kz = kk * dot(d,a);      

    float res = 0.0;

    float p = ky - kx*kx;
    float p3 = p*p*p;
    float q = kx*(2.0*kx*kx - 3.0*ky) + kz;
    float h = q*q + 4.0*p3;

    if( h>=0.0 ) 
    {   // 1 root
        h = sqrt(h);
        vec2 x = (vec2(h,-h)-q)/2.0;
        vec2 uv = sign(x)*pow(abs(x), vec2(1.0/3.0));
        float t = clamp( uv.x+uv.y-kx, 0.0, 1.0 );
        res = dot2(d+(c+b*t)*t);
    }
    else 
    {   // 3 roots
        float z = sqrt(-p);
        float v = acos(q/(p*z*2.0))/3.0;
        float m = cos(v);
        float n = sin(v)*1.732050808;
        vec3  t = clamp( vec3(m+m,-n-m,n-m)*z-kx, 0.0, 1.0 );
        res = min( dot2(d+(c+b*t.x)*t.x),
                   dot2(d+(c+b*t.y)*t.y) );
        // the third root cannot be the closest. See https://www.shadertoy.com/view/4dsfRS
        // res = min(res,dot2(d+(c+b*t.z)*t.z));
    }
    
    return sqrt( res );
}

粗判定

考虑到一些应用场景，比如判断是否点中曲线，可以通过计算点到曲线的最短距离是否小于判定距离。但在点击点到曲线距离较远的情况下，可以明显得出是否点中曲线的判断结果，在此场景下，出于性能优化考虑，对点击点先进行粗判断，在粗判断成功后才开始计算点到曲线的最短距离。

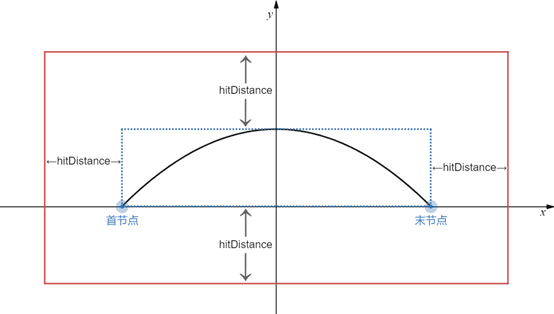
以二阶贝塞尔的首末节点连线与中垂线建立坐标系，可以得到一个正好将此贝塞尔曲线包含在内的矩形(上图内部蓝色矩形)，在此矩形基础上各个边向外扩大一个判定距离，可以得到一个更大的矩形(上图外部红色矩形)。易知红色矩形外的点到此曲线的距离一定大于判定距离，判断点是否在此矩形外即可。

粗判断的部分代码实现如下：

// 根据坐标系的偏移和旋转生成坐标映射函数
function transformCoord(rotation: number, dx: number, dy: number) {
  const cos = Math.cos(rotation);
  const sin = Math.sin(rotation);
  return function transformPoint(x, y) {
    return {
      x: cos * (x - dx) + sin * (y - dy),
      y: -sin * (x - dx) + cos * (y - dy),
    };
  };
}
// 根据dx和dy计算角度
function calculateRotation(dx: number, dy: number) {
  return Math.atan2(dy, dx);
}

const sorter = (a: number, b: number) => a - b;
// 根据贝塞尔曲线创建粗判断函数
function createIsRoughHit(fromX, fromY, cpX, cpY, toX, toY) {
  const transform = transformCoord(
    calculateRotation(toX - fromX, toY - fromY),
    (fromX + toX) / 2,
    (fromY + toY) / 2
  );
  const t_from = transform(fromX, fromY);
  const t_cp = transform(cpX, cpY);
  const t_to = transform(toX, toY);
  const ratio = Math.abs(t_from.x);
  const [bottom, top] = [t_cp.y / 2, 0].sort(sorter);
  let left, right;
  // 左右侧范围可根据数学公式求出
  if (t_cp.x >= t_from.x && t_cp.x <= t_to.y) {
    [left, right] = [t_from.x, t_to.x];
  } else if (t_cp.x > 0) {
    [left, right] = [t_from.x, 0.5 * (t_cp.x + (ratio * ratio) / t_cp.x)];
  } else {
    [left, right] = [0.5 * (t_cp.x + (ratio * ratio) / t_cp.x), t_to.x];
  }
  // 返回粗判断比对函数
  return function isRoughtHit(x: number, y: number, distance: number) {
    const t_point = transform(x, y);
    if (t_point.x < left - distance || t_point.x > right + distance)
      return false;
    if (t_point.y < bottom - distance || t_point.y > top + distance)
      return false;
    return true;
  };
}

具体实现效果

github地址
 codepen展示
性能暂未测试，实际使用较为出色，但应还有不少优化空间。

引言